Abstact

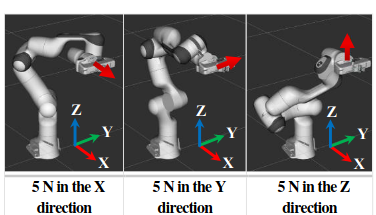
The goal of this study is to find an optimal and robust solution for on-line hierarchical least-squares optimization subject to both equality and inequality constraints. We focus on the reasoning about the task regularization to ensure the convergence and robustness of a solution in the face a singularity. The mixed problem of a regularization and inequality-constrained hierarchical optimization is not fully discussed due to the mathematical complexity. We address this problem by formulating a regularized hierarchical quadratic programming. The solution is obtained in a unified and computationally efficient manner by leveraging a singular value decomposition and an active set method. At the same time, we concentrate on the realization of the proposed algorithm as a practical means of real-time whole-body motion generation. The effectiveness of the algorithm is validated through extensive numerical simulations and experimental tests of a rescue robot successfully executing manipulation missions in a highly unstructured environment.

PDF

PDF file